Física

Resistores

 Se ainda não sabe direito o porquê de um resistor diminui a corrente elétrica vou explicar…

Ele faz isso porque ele transforma energia elétrica em energia térmica.

Entendeu?

Não?

Lê de novo!

Pra saber o valor de um resistor têm-se essa fórmula:

                                                  U=R.i

U:ddp [V (volt)]

R:resistor [Ω (ôhm)]

i:corrente elétrica [A (ampère)]

Na física,um resistor é representado dessas duas maneiras:

Exemplo:

-Determine a ddp que deve ser aplicada a um resistor ôhmico* de resistência 6Ω para ser atravessado por uma corrente elétrica de intensidade 2A:

daqui já dá pra anotar os dados:

U:?

R:6Ω

i:2A

usando a fórmula:

U=R.i

U=6.2 

U=12V

*Resistor ôhmico é aquele que o U é diretamente proporcional a  corrente i ou seja: R = U/i

——————————

Gráfico de um resistor:

Dá um close nesses gráficos:

Alguém poderia dizer qual resistor é ôhmico???escreva aqui embaixo:

_____________________________________________________________________ 

terá coragem de escrever no seu monitor?Não sei…

os gráficos 2,4,8,16 são ôhmicos porque a ddp vai ser diretamente proporcional a corrente.

Exemplo:

qual o valor da resistência nos locais marcados??

primeiro vamos marcar cada ponto desses,respectivamente por R1,R2,R3,R4, de baixo pra cima.Calculando dá:

R1:1/0,1=10Ω  R2:2/0,2=10Ω  R3:3/0,3=10Ω  R4:4/0,4=10Ω

Olhando esse outro gráfico:

calcular a resistência nesses pontos aí dá:

3,70/0,5=7,4Ω  6,18/1,0=6,18Ω  9,16/2,0=4,58Ω  11,44/4,0=2,86Ω      

De cara já dá pra ver que esse resistor não é ôhmico.

———-

Resistividade:

A resistência de um resistor depende também da forma do fio,pra isso,tem essa fórmula:

                                                                R=ρ.L/A

R:resistor (Ω)

ρ:(lê-se rô)resistividade do material do fio[Ω.m,Ω.cm,…(lê-se,respectivamente: ohm.metro,ohm.centímetro,…)]

L:comprimento do fio(m,cm,…)

A:área do fio(m²,cm²,…)

Exemplo:

-Calcule a resistência elétrica de um fio de cobre,utilizado em instalações domiciliares,de 60m de comprimento e 3mm² de área da seção transversal.A resistividade do cobre é igual a 1,7.10^-8 Ω.m.

anotando os dados:

R:?

L:60m

A:3mm²*

ρ:1,7.10^-8 Ω.m

*como a área tá em milímetros quadrados,tem que transformar pra m²:

3mm²=0,000003m² ou 3.10^-6m²

Usando a fórmula:

R=ρ.L/A

R=1,7.10^-8.60/3.10^-6

R=1,7.10^-8.20/10^-6      

R=34.10^-8/10^-6

R=34.10^-2

R=0,34Ω

—————

Associação de resistores:

Em um circuito é possível organizar conjuntos de resistores interligados, chamada associação de resistores. O comportamento desta associação varia conforme a ligação entre os resistores, sendo seus possíveis tipos: em série, em paralelo e mista.

Associação em série:

Como só tem um caminho pra corrente passar,na associação em série a corrente é igual pra todos,cada resistor tem sua ddp e valor específico.

Os resistores em série podem ser substituídos por um resistor equivalente a eles,portanto:

                                             Req=R1+R2+R3+…+Rn

Obviamente,o valor do resistor equivalente é em ohm(ah vá!).

Exemplo:

-Considere a asociação em série.Sejam R1 = 2Ω,R2 = 4Ω e R3 = 6Ω,a ddp U entre os extremos A e B da asociação é de 36V.Determine:

a)a resistência equivalente à associação

b)a ddp entre os terminais de R2.

Começando pelo item “a”,porque eu quero…os resistores estão em série,para descobrir o Req:

Req=R1+R2+R3

Req=2+4+6

Req=12Ω

Agora o item “b”

como já descobrimos o Req,ele quer saber a ddp do resistor 2,mas falta descobrir a corrente que passa por,ele,como já disse,na associação em série a corrente é a mesma,então

U=R.i

36*=12.i

i=36/12

i=3A

*lembrando que o 36 é a ddp da associação completa

descoberta a corrente:

U2=R2.i

U2=4.3

U2=12V

——————-

Associação em paralelo:

Diferente da associação  em série,quando estão associados em paralelo,a corrente de divide porque não existe somente um fio,mas ele têm em comum a ddp.

Para calcular a resistência equivalente é:

                                                   Req=R1.R2/R1+R2

Quando tiver mais de dois resistores,calcula-se dois resistores(escolhe os que tu quiser calcular)primeiro,em seguida,resolve o resistor equivalente mais o terceiro.

assim:

                                                Req’=Req.R3/Req+R3

Quando os resistores estão em paralelo,mas são iguais,o resultado será a metde:

                                                   Req=R.R/R+R=R/2

Exemplo:

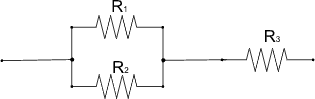
-observando o esquema abaixo,sabendo que R1=10Ω,R2=15Ω,i2=10A e i3=25A.Determine:

a)a resistência elétrica R3.

b)a intensidade da corrente elétrica i1.

c)a resistência equivalente a associação.

a)Como eu vou saber o valor de R3 se eu não tenho o valor dele e nem da ddp,só a da corrente?Se a ddp é igual pra todos,pode descobrir a ddp de outro resistor e com o valor da corrente i3,e depois,descobrir o valor de R3:

U=R2.i2  U=15.10  U=150V

agora que já tenho o valor da ddp e da corrente i3…

U=R3.i3   150=R3.25   R3=150/25   R3=6Ω

b)como já tenho o valor da ddp e de R1…

U=R1.i1   150=10.i1   i1=150/10   i1=15A

c)Descobrindo o Req,vou escolher o R1 e R3 primeiro:

Req=10.6/10+6

Req=60/16

Req=3,75Ω

Agora com o valor de um,posso descobrir o valor de outro:

Req’=3,75.15/3,75+15

Req’=56,25/18,75

Req’=3Ω

————

Associação mista:

Se tu achar que a coisa complica agora,vai se tratar…

A teoria é a mesma de antes.

Exemplo:

-Determine a resistência equivalente da associação acima com os valores:

R1:6Ω

R2:12Ω

R3:10Ω

Não te como calcular em série primeiro,porque eles não estão no mesmo fio

então calcula primeiro R1 e R2:

Req=6.12/6+12

Req=72/18

Req=4Ω

Agora  é só calcular o resto:

Req’=4+10

Req’=14Ω